Shostack + Friends Blog Archive

Is risk management too complicated and subtle for InfoSec?

In his blog [link to http://superconductor.voltage.com/ no longer works], Luther Martin has been advising caution about the use of risk assessment and risk management methods for information security. In many posts, he’s out-right skeptical, and seems to be advising against it.  Here’s the most recent example, from the post “The two-envelope problem in risk management” [link to http://superconductor.voltage.com/2009/09/the-twoenvelope-problem-in-risk-management.html no longer works] [emphasis added]:

Does it make sense to never change your information security strategy? That’s a possible consequence of the so-called two-envelope paradox. This is a problem in probability theory that has confused students of probability theory for over 50 years.

[explanation of the problem and how it applies to InfoSec investments]

The bottom line is probably that probability is a complicated and subtle concept, which means that risk management, which relies on it, also is.

Luther and I agree on his bottom-line statement.  This stuff can be complicated and subtle.  It is easy for college-educated professionals and executives to make mistakes that lead to erroneous conclusions.  In fact, Luther’s own blog post is a case study in how easy it is to make mistakes.  

Luther uses the “Two Envelopes Problem” in probability theory as an example where Bayesian (subjectivist) probability methods seem to break down in paradox.  Here’s the problem and paradox, leaving out the math for now  (details at the end):

The player is given two indistinguishable envelopes, each of which contains a positive sum of money. One envelope contains twice as much as the other. The player may select one envelope and keep whatever amount it contains, but upon selection, is offered the possibility to take the other envelope instead [“switch”]. 

[…Bayesian analysis, leading to the decision to “switch”, and then “switch” again, ad infinitum…]

As it seems more rational to open just any envelope than to swap indefinitely, the player is left with a paradox.

Following Wikipedia, Luther points out that “There’s a problem with this argument, of course, but it’s fairly subtle. Even specialists in probability theory don’t agree what the problem actually is,…”.  Luther then applies Two Envelopes Problem structure to an analogous problem in information security (I’ll call it “Two Technologies”):

Now let’s suppose that we can’t find a flaw in the above argument and we apply it to our information security strategy. Let’s suppose that we have some initial set of technology, policies and procedures that end up giving us some exposure to risk that we’ll denote R, and if we change to a different set of technology, policies and procedures, we might either increase the risk to 2R or decrease it to R/2. If we apply the same reasoning that we applied above, we find that it never pays to change, because the alternative always has a greater than the risk than what we have now. This clearly doesn’t make sense, but it’s what you might get if you do a risk analysis that isn’t as careful as it could be.

This seems OK on the surface, but Luther has made a mistake in framing the Two Technologies problem.  Simply put, his Two Technologies problem is not structured the same as the Two Envelopes problem.  Therefore Bayesian formulas for the Two Envelopes does not fit his Two Technologies problem.  Even if it did, a proper framing of the Bayesian analysis avoids the paradox. (For math details, see below).

So, yes, probability and risk management can be complicated and subtle.  But Luther’s use of the Two Envelopes Problem and his attempt to construct the same problem in InfoSec only supports this conclusion through the “covert channel” of his own mistakes.   

Is Luther implying that we shouldn’t even try risk assessment and management because it’s beyond our ken?  “Yes” seems to be the answer, if I understand his posts in the “risk” category [link to http://superconductor.voltage.com/risk/ no longer works].   What alternative to risk management is Luther proposing?  In another post [link to http://superconductor.voltage.com/2009/03/which-keeps-you-drier-walking-or-running-in-the-rain-it-turns-out-that-doing-a-careful-analysis-of-this-problem-isnt-tha.html no longer works], he suggest that we should just use trial-and-error to muddle through:

In the absence of reliable risk information, a similar approach to information security may be the best that we can do – just try different things and see which works the best. You might call this approach “experimental security.” There may be no better approach.

If someone can prove that risk assessment/management for InfoSec is impossible in principle, then Luther would be right.  But I know of no such proof of impossibility.  Just because we currently find risk management to be “complicated and subtle” doesn’t mean we should dump it.  We do need tools and frameworks that are up to the job and sufficiently usable to help ordinary people avoid the paradoxes and ratholes in the analysis.   As our academic colleagues would say: “further research is needed”.

(For mathematical details, read on…)

Mathematics of the Two Envelopes Problem, and a Solution

Luther describes the Two Envelopes Problem, then frames it using Bayesian (subjectivist) probability:

Suppose that you’re given two envelopes and you’re told that one envelope contains twice as much money as the other. You then open one of the envelopes and see how much money it contains. Based on this information, you decide to either keep the contents of the first envelope or to switch its contents for the contents of the second, unopened envelope.

It might seem that it always pays to switch.

Suppose you find $2 in the first envelope. You know that the other envelope either contains $1, which happens with probability 0.5, or it contains $4, which also happens with probability 0.5. So you can calculate the expected value of the second envelope as $1 x 0.5 + $4 x 0.5 = $2.5. Because this is greater than $2, it always pays to switch.

The paradox arises because the same logic applies after your first switch (assuming you don’t open the second envelope), which justifies a switch back to the first, and so on, ad infinitum.  The Wikipedia article lists several proposed solutions, but it may be hard for non-specialists to pick one over the other.  You might conclude that the solutions make the analysis more arcane and therefore less usable.  That may be true as long as you stick with the basic Bayesian formulation.

However, reframed in terms of “possible worlds”, the Two Envelopes Problem ceases to be a paradox.  (For a thorough explanation of this approach, see: “A Logical Approach to Reasoning About Uncertainty: A Tutorial“, by Joseph Halpern).    Here are the instructions:

1.  There are two envelopes, labeled arbitrarily “a” and “b”
2. Contents of a =X or 2X  (X is constant but unknown)
3. Contents of b =X if a=2X, else b =2X
   Thus, there are two possible worlds:
   W1: a =2X , b =X
   W2: a =X , b =2X
4. p = subjective probability or belief in a possible world
5. Pick a, and open it
6. Decide whether to keep a or switch to b

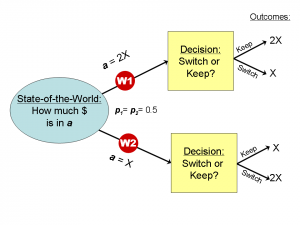
Possible worlds framework for Two Envelopes Problem

There are two decision alternatives to evaluate over the possible worlds: “keep” and “switch”.  To evaluate each alternative, trace each possible world path and multiply the outcome value by the subjective probability of that possible world (which, in this case, is identical for each = 0.5, because of no prior information):

• “Keep” outcome    = p(W1)* 2X + p(W2) * X  = 0.5 * 2X + 0.5 * X = 1.5X
• “Switch” outcome = p(W1)* X + p(W2)* 2X  =  0.5 * X + 0.5 * 2X = 1.5X

Result: the expected value for each of these decision alternatives is the same, 1.5X, which is the average value of the two envelopes.  Thus, you are indifferent on whether you should “keep” or “switch”, which matches common sense, absent any other information.

Very important to this analysis is that the actual dollar value revealed when you open the first envelope is not informative.  This should be a red flag when someone proposes to name a variable set to that value, as was done in the Bayesian analysis in the Wikipedia article, and also Luther’s post.

Mathematics of Luther’s “Two Technologies” Problem

Again, here is Luther’s description:

Now let’s suppose that we can’t find a flaw in the above argument and we apply it to our information security strategy. Let’s suppose that we have some initial set of technology, policies and procedures that end up giving us some exposure to risk that we’ll denote R, and if we change to a different set of technology, policies and procedures, we might either increase the risk to 2R or decrease it to R/2. If we apply the same reasoning that we applied above, we find that it never pays to change, because the alternative always has a greater than the risk than what we have now. This clearly doesn’t make sense, but it’s what you might get if you do a risk analysis that isn’t as careful as it could be.

Here are the instructions for framing the Two Technologies problem in terms of possible worlds:

1. There exists a new incremental investment in information security technology, T
2. Information security risk is r = probability of breach * loss due to breach
3. Without T, r=R (a constant)
4. With T, r= R/2 or 2R
   Thus, there are three possible worlds :
   W0: r=R
   W1: r= 2R
   W2: r= R/2
5. p = subjective probability or belief in a possible world
6. Decide whether to invest in T 

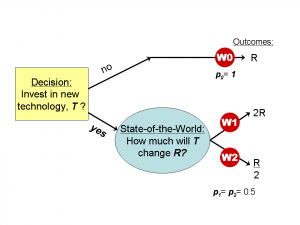
Possible Worlds framework for Two Technologies Problem

There are two decision alternatives to evaluate over the possible worlds: “No T”  (don’t invest) and “Yes T” (do invest).  To evaluate each alternative, trace each possible world path and multiply the outcome value by the subjective probability of that possible world:

• “No T” outcome   r = p(W0)* R  = 1 * R = R
• “Yes T” outcome r = p(W1)* 2R + p(W2)* R/2  =  0.5 * 2R + 0.5 * R/2 = 1.25R

Result: the expected value “No T” (don’t invest) is R, which is less than the expected value of “Yes T” (do invest).  Therfore, don’t invest in the new technology.  This is the result that Luther reported in his post.

(Note: p sums to 1 for sets of possible worlds that are mutually exclusive, given any preceding decisions.  In this problem, there are two sets of mutually exclusive possible worlds: 1) W0 and 2) W1, W2.)

Here’s what’s wrong:  Luther made some errors in defining the Two Technologies problem, as you can see from a quick comparison of the two diagrams. They are not the same problems at all!  Specifically, there are three errors that make these different problems:

1. The decision variable comes after the state-of-the-word variable in the Two Evelopes problem, while in Luther’s Two Technologies problem they are reversed. 
2. More important, there is no uncertainty if the decision is “No T“.  The level of risk is deterministic.  This makes the problem different than Two Envelopes, where symmetrical uncertainty exists for both decision alternatives. 
3. Finally, impact of technology T on risk r is defined to be superficially similar to the Two Envelop problem with two possibilities: 1) risk is doubled or 2) risk is cut in half.   It is as if Luther is trying to embed the Two Envelopes problem inside the Two Technologies problem, but only along one decision path.   If, instead, the same uncertain state-of-the-world existed on both decision paths, then the results would have been the same as Two Envelopes problem we saw above: outcome values are the the same for both decision alternatives. 

If you think about the Two Technologies problem in simple language, then it becomes obvious why the new technology investment is unjustified.  Who would invest in security technology that has an equal chance of either reducing InfoSec risk by 50% or increasing it by 100%?  Change those risk impact possibilities to something more reasonable, like “no impact” vs. “50% reduction”, and the investment looks justified.  The Two Envelopes Problem is irrelevant in this case.

Conclusion

I hope I’ve been able to convince you that the Two Evelope problem really doesn’t say anything significant about information security risk management decision, and that Luther made some mistakes in trying to create an analogous Two Technologies problem. 

I also hope that this demonstration will help anyone who might be doing InfoSec risk analysis, especially how to frame the problem in a way that accounts for various forms of uncertainty, decisions, etc.  In addition to the Halpern referenced above, I also recommend his book: Reasoning About Uncertainty, MIT Press, 2003. Paperback issue published in 2005.

(Caution: This isn’t a simple how-to book. This book is fairly advanced, technical, and academic, though some of the introductions are fairly accessible to the non-specialist.  If you want to dip into specific topics, you can go to Halpern’s publication page.  However, these are almost all academic papers, which can be hard to read by non-specialists. 

If you are among the people who think probability, even Bayesian probability, is the be-all and end-all for reasoning about risk and uncertainty, then this material will hit you like a cold shower!)

Originally published by Russell on 13 Sep 2009
Last modified on 13 Sep 2009
Categories:   Science of Risk Management   Uncategorized